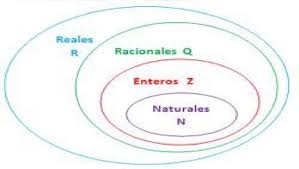
CONSTRUCCIÓN DE LOS CONJUNTOS
NUMÉRICOS
1. EL CONJUNTO DE
LOS NÚMEROS NATURALES
a. Equipotencia de conjuntos.- Dos
conjuntos son equipotentes cuando tienen la misma cantidad de elementos.
De
esta manera se forma un conjunto universo donde cada subconjunto está formado
por conjuntos equipotentes. A cada subconjunto se denomina “Clase de
Equivalencia”, y se le da un nombre: UNO a la clase de conjuntos que tiene un
solo elemento, su símbolo es “1” .
DOS a la clase de conjuntos que tiene dos elementos. Sun símbolo es “2” . TRES a la clase de conjuntos
que tiene tres elementos. su símbolo es “3” . y así sucesivamente.
b. De esta forma se constituye el conjunto
de números naturales N.
2. EL CONJUNTO Z DE
LOS NÚMEROS ENTEROS
El conjunto de números
enteros es una ampliación del conjunto de números naturales. Apareció para
resolver el problema de la resta de naturales.
El problema era el
siguiente, por ejemplo: Si se tiene la siguiente resta:
4 – 7 = ?
¿Cuál es el resultado? Pues,
no hay en el resultado en el conjunto de los números naturales. Es decir, la
adición de naturales no cumple la propiedad interna o cde clausura, y de ese
modo aparecieron los números negativos. En el resultado anterior el resultado
será:
4 – 7 = -3
Entonces, si los números
naturales son los positivos:
El
conjunto de los números racionales aparece por causa de la imposibilidad de la
operación de división con números enteros, por ejemplo:
5 / 7 = ¿? No
existe resultado en los Z
Por
lo tanto, La operación de división tampoco cumple la propiedad interna o
cerrada, es por eso que esta operación queda indicada como 5/7 , y de esta
forma aparecen los números racionales o “quebrados”
4. EL CONJUNTO DE LOS NÚMEROS REALES
4. EL CONJUNTO DE LOS NÚMEROS REALES
El conjunto de los
números reales aparece por causa de que algunos números son imposibles de
representarlos en forma de fracción o quebrado, por ejemplo √2, √3, √5, el
número “e” (que se usa en los logaritmos), el número pi (“π”), etc. Es así
que a todo este conjunto de números se
denomina “irracionales”, porque no se los puede escribir en forma de una razón
o racional.
BIBLIOGRAFÍA
- Santillana 1° de secundaria, año 2010
- Hoguera 6° de primaria, año 2012