3. ADICIÓN DE NÚMEROS ENTEROS

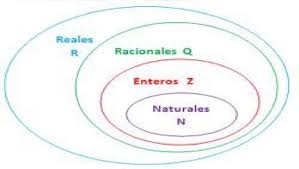
NÚMEROS ENTEROS

  

Los números enteros son un conjunto de números que incluye a los números naturales distintos de cero (1, 2, 3, ...), los negativos de los números naturales (..., −3, −2, −1) y al 0.

I. ADICIÓN DE NÚMEROS ENTEROS

A. ADICIÓN DE ENTEROS DEL MISMO SIGNO

¡Muy elemental! Se suman los números y el resultado lleva el mismo signo.

 

 B. ADICIÓN DE ENTEROS DE SIGNO DIFERENTE

¡La mayoria manda!

Se restan  y el resultado lleva el signo  del “mayor”.     

 

C. PROPIEDADES DE LA ADICIÓN DE ENTEROS

1. Propiedad Interna

Cuando se suman dos números enteros, el resultado es otro número entero. en símbolos:

" a, b Î Z  a + b = c à  c Î Z

2. Propiedad asociativa

La suma de dos o más números perimte asociar los sumandos,

(a + b) + c = (a + b) + c

3. Propiedad del elemento neutro

Todo entero sumado con el neutro es el mismo número entero.

" a Î Z,   a + 0 = a

El neutro aditivo en este caso es el cero, porque todo entero sumado con el cero es el mismo entero.

4 Propiedad del elemento inverso

Para todo entero que sumado con su inverso, da el elmento neutro.

" a Î Z, $ (-a) ,  a + (- a) = 0

 

BIBLIOGRAFÍA

-      Santillana 1° de secundaria,  año 2010
-    Hoguera 6° de primaria, año 2012
-   A.Baldor; Aritmética

2. CONJUNTOS NUMÉRICOS

CONSTRUCCIÓN DE LOS CONJUNTOS NUMÉRICOS

 

1. EL CONJUNTO DE LOS NÚMEROS NATURALES 

 

a. Equipotencia de conjuntos.- Dos conjuntos son equipotentes cuando tienen la misma cantidad de elementos.

De esta manera se forma un conjunto universo donde cada subconjunto está formado por conjuntos equipotentes. A cada subconjunto se denomina “Clase de Equivalencia”, y se le da un nombre: UNO a la clase de conjuntos que tiene un solo elemento, su símbolo es “1”. DOS a la clase de conjuntos que tiene dos elementos. Sun símbolo es “2”. TRES a la clase de conjuntos que tiene tres elementos. su símbolo es “3”. y así sucesivamente.

 

b. De esta forma se constituye el conjunto de números naturales N.

 

2. EL CONJUNTO Z DE LOS NÚMEROS ENTEROS

El conjunto de números enteros es una ampliación del conjunto de números naturales. Apareció para resolver el problema de la resta de naturales.

El problema era el siguiente, por ejemplo: Si se tiene la siguiente resta:

4 – 7 = ?

¿Cuál es el resultado? Pues, no hay en el resultado en el conjunto de los números naturales. Es decir, la adición de naturales no cumple la propiedad interna o cde clausura, y de ese modo aparecieron los números negativos. En el resultado anterior el resultado será:

4 – 7 = -3

Entonces, si los números naturales son los positivos:

 

 

Este conjunto se simboliza con la letra Z.Cuando un número entero no lleva signo, se sobreentiende que es positivo. 3. EL CONJUNTO DE LOS NÚMEROS RACIONALES "Q"

El conjunto de los números racionales aparece por causa de la imposibilidad de la operación de división con números enteros, por ejemplo:

5 / 7  =  ¿?     No existe resultado en los Z

 

Por lo tanto, La operación de división tampoco cumple la propiedad interna o cerrada, es por eso que esta operación queda indicada como 5/7 , y de esta forma aparecen los números racionales o “quebrados”

 
4. EL CONJUNTO DE LOS NÚMEROS REALES "R"

El conjunto de los números reales aparece por causa de que algunos números son imposibles de representarlos en forma de fracción o quebrado, por ejemplo √2, √3, √5, el número “e” (que se usa en los logaritmos), el número pi (“π”), etc. Es así que  a todo este conjunto de números se denomina “irracionales”, porque no se los puede escribir en forma de una razón o racional.

 

 

BIBLIOGRAFÍA

-      Santillana 1° de secundaria,  año 2010

-      Hoguera 6° de primaria, año 2012

1. SISTEMAS DE NUMERACIÓN ANTIGUA

SISTEMAS DE NUMERACIÓN ANTIGUA

Entre los sistemas antiguos:

1.    Sistema Egipcio

Su sistema de numeración era de base diez, como el nuestro. Los símbolos para representar las potencias de 10 eran estos:

Cada símbolo podía repetirse hasta nueves veces carecían de valor posicional.

2.    Sistema Babilónico

Los babilonios empleaban un sistema sexagesimal posicional adaptado tras tomar el de los sumerios y también de la civilización de Acadia. Los números babilónicos se escribían en cuneiforme, usando una aguja de lámina inclinada para acuñar marcas en unas tablas de arcilla suave que luego se exponían al sol para endurecerlas y que quedasen permanentemente.

Este sistema apareció por vez primera alrededor de 1900-1800 a. C. También se acredita como el primer sistema de numeración posicional.

3.    Sistema Maya

Los Mayas desarrollaron su escritura  numérica  jeroglífica,  o sea con símbolos propios para los números. Primeramente utilizaron un sistema numérico  no  decimal,  no  posicional  que  tuvo  poca trascendencia. En el emplearon el cero, pero no el  principio  del valor de los números por su posición; usando  símbolos  especiales para  denotar  las  diferentes  unidades.  Era  como  si  nosotros fuéramos a escribir en  nuestro  sistema  el  número  460  como  4 centenas, 6 decenas y 0 unidades; que por supuesto es  equivalente a decir 6 decenas, 0 unidades y 4 centenas; sin que el  cambio  de posición influya en el resultado final. Sistemas similares también se encuentran en los albores de otras civilizaciones.

El segundo sistema numérico, desarrollado por los calculadores del Calendario de esta Antigua Civilización de América Central fue introducido entre los siglos IV y III AC. con base 20, por lo que tampoco fue un sistema decimal. En el emplearon el principio  de la posición y el cero, para el que tenían un  símbolo  parecido  a una concha de mar en la forma.

 

Además tenían nueve  ordenes  de unidades.

BIBLIOGRAFÍA:http://www.aula365.com/post/sistemas-numeracion/           

http://www.tareasya.com.mx/index.php/tareas-ya/secundaria/matematicas/aritmetica/2098-Sistemas-de-numeraci%C3%B3n-egipcio,-babilonio-y-romano.html